ลำดับ

ลำดับ (Sequence)

เราคง เคยเห็นข้อสอบวัดไอคิว อาจเคยเห็นข้อสอบ ประเภทให้ตัวเลขมา 3-4 ตัว แล้วถามว่า ตัวเลขถัดไปจะเป็นอะไร ตัวอย่างเช่น 1, 2, 4, 7, .... แล้วตัวต่อไปจะเป็นอะไร จากนั้นก็จะมีการพัฒนาข้อสอบเป็น ลำดับรูปภาพต่าง ๆ ให้ได้คิดกัน นอกจากนี้ ในชีวิตประจำวันของ ยังคุ้นเคยกับคำว่า ลำดับ คือ การเรียงกันของสิ่งของ หรือเหตุการณ์ต่าง ลำดับตัวเลข คือ ฟังก์ชันที่นิยามบนเซต ของจำนวนเต็มบวก ตัวเลขในลำดับแต่ละตัวเรียกว่า พจน์ (term)” หรือเราสามารถนิยามได้ว่า ลำดับ คือเซตของจำนวนที่เรียงเป็น a₁,a₂,a₃,... โดยมีการเรียงที่เป็นแบบแผนขั้นตอน เลขที่ห้อยอยู่บอกถึงตำแหน่งของเลขในลำดับนั้น

ตัวอย่างเช่น 1,3,5,7,... และ 2,4,8,16,...

จากตัวอย่างที่ 1 เลขลำดับที่ 1 คือ 1, ลำดับที่ 2 คือ 3, ลำดับที่ 3 คือ 5, . . .,

แล้ว เราสามารถหารูปแบบได้ว่า ลำดับที่ n^th (a_n) คือ 2n-1 ได้อย่างไม่ยาก

ส่วนตัวอย่างที่ 2 เลขลำดับที่ 1 คือ 2, ลำดับที่ 2 คือ 4, ลำดับที่ 3 คือ 8, . . ., แล้ว

เราสามารถหารูปแบบได้ว่า ลำดับที่ n^th (a_n) คือ 2ⁿ ได้อย่างไม่ยากเช่นกัน การเขียนแทนลำดับนอกจาก a₁,a₂,a₃,...,a_n,... หรือ{ a₁,a₂,a₃,...,a_n,...} แล้ว เรายังสามารถเขียนได้ในรูป

หรือ {a_n} เรียกว่า “Bracket notation”

ซึ่งแทนลำดับที่มีพจน์ทั่วไป เป็น a_n

เรียก a₁ ว่าพจน์ ที่ 1 ของลำดับ

เรียก a₂ ว่าพจน์ ที่ 2 ของลำดับ

เรียก a₃ ว่าพจน์ ที่ 3ของลำดับ

เรียก a_nว่าพจน์ ที่ n ของลำดับ

จะเห็นได้ว่าลำดับเป็นเซตของจำนวนที่เรียงลำดับกันภายใต้กฎเกณฑ์ อย่างใดอย่างหนึ่งร่วมกัน

ลำดับที่มีพจน์เป็นจำนวนจำกัด เรียกว่า ลำดับจำกัด ( Finite Sequence )

ลำดับที่มีจำนวนพจน์ ไม่จำกัด เรียกว่า ลำดับอนันต์ ( Infinite Sequence )

การกำหนดลำดับหนึ่ง มักจะบอกโดยสูตร สำหรับพจน์ที่ n ในลำดับนั้น เช่น ลำดับ 2 ,4,6,8,...

อาจจะบอก โดย 2,4,6,8,...2n,.... เมื่อ n เป็นจำนวนเต็มบวกหรือเขียนให้กระชับขึ้น

โดยใช้สัญลักษณ์

ในสัญลักษณ์ นี้ แต่ละพจน์เกิดจากการแทนจำนวนเต็ม

n = 1,2,3,... ลงในสูตร 2n

ตัวอย่าง 1 จงเขียน 5 พจน์แรกของลำดับ

วิธีทำ แทน n = 1,2,3,4,5,... ลงในสูตร 2ⁿ

ได้ 2¹ , 2², 2³, 2⁴, 2⁵, . . . หรือ 2,4,6,8,..,32,...

ตัวอย่าง 2 จงเขียนลำดับต่อนี้ในรูป Bracket notation

(ก)

ตอบ

(ข)

ตอบ

(ค) 1,-1,1,-1,...
ตอบ

(ง)

ตอบ

(จ) 1,3,5,7,...
ตอบ {2n-1}

ข้อสังเกต อักษร a และ n อาจจะใช้ตัวอักษร อื่นแทนได้ เช่น a_n อาจจะแทนด้วย b_k ก็ได้
จากที่กล่าวมาข้างต้นจะเห็นว่าในการเขียนลำดับ 2,4,8,16,32,...,2ⁿ,...หรือ

เป็นการกำหนดความเกี่ยวข้องระหว่างจำนวน 2ⁿ และจำนวนเต็มบวก n ซึ่งกล่าวได้อีกแบบหนึ่งว่า

เป็นสูตรสำหรับฟังก์ชันที่มีตัวแปรอิสระคือ n แปรค่าบนจำนวนเต็มบวก

ดังนั้น อาจจะเขียน ในรูปฟังก์ชันเป็น f(n) = 2ⁿ , n = 1,2,3,... และ 2,4,8,16,32,...,2ⁿ,... แทน
ฟังก์ชัน f(1) , f(2) , f(3) , ... f(n) , ...

เนื่องจากทุกลำดับมีโดเมน คือ เซตของจำนวนเต็มบวกเหมือนกัน ดังนั้น ต่อไปจะเขียน {a_n}
แทน

หรือ {f(n)} แทน

ลำดับอนันต์ (Infinite Sequence) คือ ลำดับที่ไม่มีจุดจบ

เช่น ลำดับของจำนวนนับ 1, 2, 3, ... ลำดับจำกัด (Finite Sequence) คือ ลำดับที่มีจำนวนพจน์จำกัด
ตัวอย่างเช่น ลำดับหน้าของหนังสือเล่มหนึ่ง

    ลำดับชนิดพิเศษ

1) ลำดับเลขคณิต (Arithmetic sequence) ลำดับเลขคณิต เป็น ลำดับเลขที่แต่ละพจน์หลังจากพจน์แรกมีค่าเพิ่มขึ้น  หรือลดลง จากพจน์หน้าที่ติดกัน ด้วยค่าต่างคงที่ เรียกว่า ผลต่างร่วมของลำดับ

ตัวอย่าง เช่น 3, 6, 9, 12, . . . เราทราบว่าลำดับนี้เป็นลำดับเลขคณิต

เพราะ มีผลต่างร่วม = 3 = 12 -9 = 9 -6 = 6 -3

ถ้าเราแทนพจน์แรกด้วย a₁, และพจน์ที่ i ด้วย a_i เราจะได้ว่า

a_i = a₁ + 3(i - 1) = 3 + (3i - 3) = 3i

ดังนั้นเราจึงมีสูตรว่า a_i = a₁ + d(i - 1) เมื่อ d แทนผลต่างร่วมของลำดับนี้

2) ลำดับเรขาคณิต (Geometric sequence) ลำดับเรขาคณิต เป็น ลำดับเลขที่แต่ละพจน์หลังจากพจน์แรกมีค่าเพิ่มขึ้น หรือลดลง โดยการคูณพจน์หน้าที่ติดกัน ด้วยค่าคงที่ เรียกว่า อัตราส่วนร่วมของลำดับ

ตัวอย่างเช่น 2, 4, 8, 16, . . .

เราทราบว่าลำดับนี้เป็นลำดับเรขาคณิต เพราะ มีอัตราส่วนร่วม = 2 = 4 / 2 = 8 / 4 = 16 / 8
ถ้าเราแทนพจน์แรกด้วย a₁, และพจน์ที่ i ด้วย a_i เราจะได้ว่า a_i = a₁r^{(i - 1}⁾ = 2(2^{(i - 1}⁾) = 2ⁱ

ดังนั้นเราจึงมีสูตรว่าa_i = a₁r^{(i - 1}⁾ เมื่อ r แทนอัตราส่วนร่วมของลำดับนี้

ลิมิตของลำดับ

ในการที่จะกล่าวว่า ลำดับ {a_n} เข้าใกล้ลิมิต L เมื่อ n มีค่ามากขึ้น นั่นหมายถึงว่าพจน์ในลำดับนั้น มีค่าเข้าใกล้จำนวน L ดังนั้น ถ้าเราเลือกจำนวนบวก e ใดๆ พจน์ต่างๆ ในลำดับนั้นจะต่างจาก L ไม่เกิน ±e

นั่นคือ ถ้าลากเส้น y = L + e และ y = L-e แล้วพจน์ในลำดับนั้นจะถูกกักอยู่ภายในแถบระหว่างเส้นทั้งสอง

นิยาม 1 จะเรียกว่าลำดับ y = L+ e มีลิมิต L ถ้ากำหนด e > 0 ใดๆ แล้วมีจำนวนเต็มบวก N โดยที่

Ιa_n – LΙ < e เมื่อ n ≤ Nถ้า ลำดับ y = L+ e มีลิมิต L แล้วเรากล่าวว่าลำดับ คอนเวอร์จ หรือลู่เข้าและเขียนแทนด้วย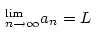

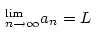และเรียกลำดับที่ไม่มีลิมิตว่า ไดเวอร์จ หรือ ลู่ออก

การคำนวนค่าลิมิตของลำดับ(Calculating limit of Sequence)

ทฤษฎีบท 2 กำหนดให้ {a_n} และ {b_n} เป็นลำดับของจำนวนจริง และ A,B,k เป็นจำนวนจริง
ถ้า

และ

แล้วจะได้ว่า

1.

( Sum Rule )

( Difference Rule )

( Product Rule )

( Constant Multiple Rule )

ทฤษฎีบท 3 ถ้าให้ ƒ(×) เป็นฟังก์ชันที่นิยามสำหรับ x > n₀ และ {a_n} เป็นลำดับของจำนวนจริง
ซึ่งทำให้ {a_n} = f (n) สำหรับ แล้วจะได้ว่า n > n₀

ถ้า

แล้ว

= L

จาก ท.บ.2 ถ้าในการคำนวณ

ได้ลิมิตอยู่ในรูป 0/0 หรือ ∞ / ∞

วิธีการแยกตัวประกอบ หรือ แยกแฟกเตอร์ ช่วยในการหาลิมิต ลำดับต่อไปนี้เป็นลำดับลู่เข้าหรือไม่?

ตอบ ลู่เข้า -6

2.

ตอบ ลู่ออก

ตอบ ลู่เข้า 1/9

4.

ตอบ ลู่เข้า 1/2

5. {Ιn n – Ιn (2n³+1)} ตอบ ลู่ออก

ในการตรวจสอบการลู่เข้าหรือลู่ออกของลำดับที่มีความซับซ้อนนั้นจำเป็นต้องหาลิมิตในรูปแบบไม่กำหนด ลักษณะต่างๆ ( ±∞/∞, 0.(±∞),0⁰ , ±∞⁰, $1^{pminfty}$ , (±∞)(±∞) )

, c > 0

5)

, c > 0

กรณี 4)-6) c เป็นค่าคงที่

โจทย์ จงทดสอบลำดับอนันต์

ตอบ ใส่ Ιn เข้าไปหน้าฟังก์ชัน

ก่อนใช้กฎโลปิตาล แล้วจะได้ว่า
ลำดับนี้ลู่เข้า e²

ทฤษฎีบท 4 ( The Sandwich Theorem of Sequence ) ให้ {a_n} และ {b_n} และ {c_n}
เป็นลำดับ ของจำนวนจริง โดยที่ a_n ≤ b_n ≤ c_nทุกๆค่า n ถ้า

แล้วจะได้ว่า

ตัวอย่าง จงแสดงว่าลำดับ

ลู่เข้า

วิธีทำ เราทราบว่า

และเพราะ

เราจึงสรุปได้ว่า

ด้วย โดยทฤษฎีบท 4

ทฤษฎีบท 5 ( The Continuous Function Theorem for sequence ) ให้ {a_n} เป็นลำดับของจำนวนจริง ซึ่ง

และ f เป็นฟังก์ชันที่ต่อเนื่อง ที่ นิยาม ที่ a_n ทุกค่า n แล้ว

หมายเหตุ อาจเขียนได้ว่า a_n → L แล้ว ƒ(a_n) → ƒ(L)

ตัวอย่าง ลำดับ

เป็นลำดับลู่เข้าหรือไม่

วิธีทำ เนื่องจาก

จึงได้ว่า

ลำดับทางเดียว

นิยาม 1 จะเรียกลำดับ {a_n} ว่า
- เป็นลำดับเพิ่ม ถ้า a₁ < a₂< a₃ < ... < a_n <...

- เป็นลำดับไม่ลด ถ้า a₁ ≤ a₂≤a₃ ≤ ... ≤ a_n ≤...

- เป็นลำดับลด ถ้า a₁ >a₂ > a3 > ... > a_n >...

- เป็นลำดับไม่เพิ่ม ถ้า a₁ ≥ a₂≥a₃ ≥ ... ≥ a_n ≥...

เรียกลำดับที่เป็นลำดับไม่ลด หรือเป็นลำดับไม่เพิ่มว่า ลำดับทางเดียว ( monotone)

และ เรียก ลำดับที่เป็นลำดับเพิ่ม หรือเป็นลำดับลดว่า ลำดับทางเดียวโดยแท้ ( strictly monotone )

นั่นคือ ลำดับทางเดียวโดยแท้ จะเป็นลำดับทางเดียวด้วย ( แต่บทกลับไม่จริง )

ตัวอย่าง 1
(1)

เป็นลำดับเพิ่ม

(2)

เป็นลำดับลด

(3) 1,1,2,2,3,3,.... เป็นลำดับไม่ลด

(4)

เป็นลำดับไม่เพิ่ม

(5) ลำดับทั้งสี่เป็นลำดับทางเดียว และลำดับ (1) , (2) เป็นลำดับทางเดียวโดยแท้ ลำดับที่ไม่เป็นลำดับทางเดียว

เช่น

การทดสอบการเป็นลำดับทางเดียว การตรวจสอบลำดับว่า เป็นลำดับเพิ่ม หรือลำดับลด อาจทำได้ดังนี้

วิธีที่ 1 พิจารณา a_n+1- a_n ถ้าพบว่า a_n+1- a_n > 0 แล้ว แสดงว่า {a_n} เป็นลำดับลด

และ ถ้าพบว่า a_n+1- a_n > 0 แล้ว แสดงว่า {a_n} เป็นลำดับเพิ่ม

วิธีที่ 2 ถ้า {a_n} เป็นลำดับที่ a_n> 0 ทุกๆ n = 1,2,3,... แล้ว

จะพิจารณาอัตราส่วน

ถ้า

ทุกๆ n= 1,2,3,...

แล้ว{a_n} เป็นลำดับลด และ ถ้า

ทุกๆ n = 1,2,3,.., แล้ว{a_n} เป็นลำดับเพิ่ม

หมายเหตุ - ถ้าเครื่องหมายใน (1) หรือ (3) เป็น ≤ จะเป็นลำดับไม่เพิ่ม
- ถ้าเครื่องหมายใน (2) หรือ (4) เป็น ≥ จะเป็นว่าลำดับไม่ลด

ตัวอย่าง 2 จงพิจารณาลำดับต่อไปนี้ว่าเป็นลำดับทางเดียวหรือไม่ ถ้าเป็น เป็นลำดับเพิ่มขึ้น หรือ ลดลง

2.1

ตอบ ใช้วิธีที่ 1 จะได้ว่า เป็นลำดับลด

2.2

ตอบ ใช้วิธีที่ 2 จะได้ว่า เป็นลำดับลด

ตัวอย่าง 3 จงแสดงว่าลำดับ

เป็นลำดับลด

วิธีทำ ใช้วิธีตรวจสอบอัตราส่วนของพจน์ที่ติดกัน

สำหรับทุกค่า n ≥ 1 เสมอ จึงสรุปได้ว่า เป็นลำดับลด

ลำดับที่มีขอบเขต

นิยาม 1 ให้ {a_n} เป็นลำดับของจำนวนจริง เรียกจำนวนจริง A ว่าขอบเขตบน ( Upper Bound ) ของ {a_n}
ก็ต่อเมื่อ a_n ≤ A สำหรับทุก ๆ n = 1,2,3,... และเรียก A ว่าขอบเขตบนค่าน้อยสุด ( Least Upper Bound ) ของ {a_n}
ก็ต่อเมื่อ A เป็นขอบเขตบนของ {a_n} และ A มีค่าน้อยกว่าหรือเท่ากับขอบเขตบนทุกตัวของ {a_n}

นิยาม 2 ให้ {a_n}เป็นลำดับของจำนวนจริง เรียกจำนวนจริง B ว่าขอบเขตล่าง ( Lower Bound ) ของ{a_n}
ก็ต่อเมื่อ B ≤ a_nสำหรับทุก ๆ n = 1,2,3,... และเรียก B ว่าขอบเขตล่างค่ามากสุด

( Greatest Lower Bound ) ของ {a_n} ก็ต่อเมื่อ B เป็นขอบเขตล่างของ {a_n} และ B มีค่ามากกว่าหรือเท่ากับขอบเขตล่างทุกตัวของ {a_n}เราจะเรียก {a_n} ว่ามีขอบเขต ก็ต่อเมื่อ {a_n} มีทั้งขอบเขตบนและขอบเขตล่าง

ตัวอย่าง 1
1.1 ลำดับ {2n} = 2,4,6,8,... มี 2 เป็นขอบเขตล่างค่ามากสุด แต่ไม่มีขอบเขตบน
ดังนั้นลำดับนี้จึงไม่มีขอบเขต และ เป็นลำดับเพิ่ม
1.2 ลำดับ {(-1)ⁿ} = -1, 1, -1,1,... มี 1 เป็นขอบเขตล่างค่ามากสุด
และ มี -1 เป็นขอบเขตล่างค่ามากสุด ดังนั้นลำดับนี้จึงมีขอบเขต แต่ลู่ออก

1.3 ลำดับ

มี -1 เป็นขอบเขตล่างค่ามากสุด และ

1/2 เป็นขอบเขตบนค่าน้อยสุด ดังนั้น

เป็นลำดับที่มีขอบเขตและ ไม่เป็นลำดับทางเดียว

ตัวอย่าง 2 พิจารณาลำดับ

ให้

ดังนั้น

จึงได้ว่า a_n+1 ≥ a_n ทุก ๆ n = 1,2,3,... นั่นคือ a₁ ≤ a₂≤ a₃ ≤ ...

หรือ

และ จะได้ว่า a_n≤ 1/3 ทุก ๆ n = 1,2,3,...

ดังนั้น 1/3 เป็นขอบเขตล่างของ{a_n} นอกจากนี้แล้วยังมีจำนวนจริงอีกมากมายที่เป็นขอบเขตล่าง ของ
{a_n} เช่น 0 , -1 ,-3/2 เป็นต้น แต่ทุกจำนวนที่เป็นขอบเขตล่างของ {a_n}จะมีค่าไม่เกิน 1/3
ดังนั้น 1/3 เป็นขอบเขตล่างที่มีค่ามากที่สุด สำหรับขอบเขตบนของ {a_n}จะพิจารณาจาก

ทุกๆ n = 1,2,3,... ดังนั้น 1/2 เป็นขอบเขตบนค่าหนึ่งของ {a_n} และ
ทุกจำนวนที่มากกว่าหรือเท่ากับ 1/2 เป็นขอบเขตบน ทั้งหมด การที่จะแสดงว่า 1/2เป็นขอบเขตบนค่า
น้อยสุดทำได้ดังนี้ สมมติว่ามีจำนวนจริง y โดยที่ 0 < y = 1/2 และ y เป็นขอบเขตบนของ {a_n}

แล้ว จะมีจำนวนเต็มบวก m ตัวหนึ่งซึ่ง